A probabilistic graphical model (PGM) is a graph formalism for compactly modeling joint probability distribuitions and (in)dependence relations over a set of random variables. A PGM is called a Bayesian Network when the underlying graph is directed, and a Markov Network is when the underlying graph is undirected. Generally speaking, you use the former to model probabilistic influence between variables that have clear directionality, otherwise you use the latter.
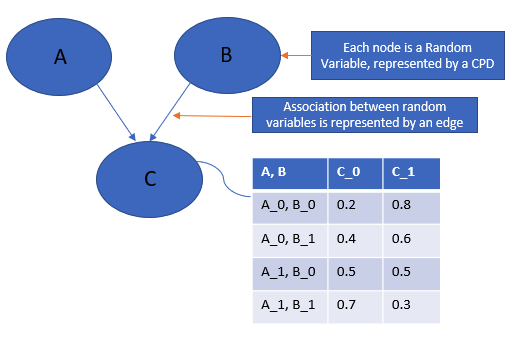
Illustration of a probabilistic graphical model between 3 random variables. In this case: a Bayesian Network as the graph is directed
The Bayesian network is a kind of PGM that uses a directed (acyclic) graph to represent a factorized probability distribution and associated conditional independence over a set of variables. The Markov process (Markov chain) is a stochastic process (typically thought of as a collection of random variables) that satisfy the Markov property (the future state only depends upon the present state and does not depend on the past state).
Note:
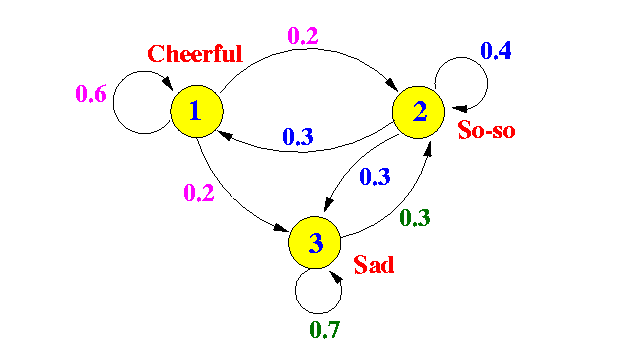
The Markov process (Markov chain) like the diagram below is not considered a PGM because the nodes are not random variables, but rather elements of the state space of the random variable chain; the edges correspond to the (non-zero) transitional probabilities between two consecutive states.
A Bayesian network is a probabilistic graphical model that represents the causal probabilistic relationship among a set of random variables, their conditional dependences, ant it provides a compact representation of a joint probability distribution. Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor.
Formally, Bayesian network are acyclic directed graph (a directed graph with no directed cycles) whose nodes represent variables in the Bayesian sense. If there exists a casual probabilistic depenence between two random variables in the graph, the corresponding two nodes are connected by a directed edge, while the directed edge from a node \(A\) to node \(B\) indicate the random variable $A$ causes the random variable \(B\), represented by the conditional probability \(P(B\mid A)\).
Example:

A simple Bayesian network with conditional probability tables
Two events can cause Grass to be wet: an active Sprinkler or Rain. This situation can be modeled with a Bayesian network. Each variables has two possitive value: True \(T\) or False \(F\).
By the chain rule of probability, the joint probability function is:
\[P(G,S,R) = P(G\mid S,R)\cdot P(S \mid R)\cdot P(R)\]The model can answer question about the presence of a coause given the presence of an effect like “What is the probability that it is raining, given the grass it wet?” \(P(R_T\mid G_T)\). By using the conditional probability formula and summing over all nuisance variables, we have:
\[P(R_T|G_T) = \frac{P(G_T, R_T)}{P(G_T)} = \frac{\sum_{x\in\{T,F\}}P(G_T, S_x, R_T)}{\sum_{x,y\in\{T,F\}}P(G_T, S_x, R_y)}\]where \(G\), \(S\), \(R\) are Grass wet, Sprinkler turn on, and Raining, where \(G_T\) is “grass wet is true”
Base on the conditional probability tables on the diagram, we can calculate individual conditional probability value, for example:
\[\begin{aligned} P(G_T, S_T, R_T) &= P(G_T|S_T,R_T)\cdot P(S_T|R_T)\cdot P(R_T) \\ &= 0.99 \times 0.01 \times 0.2 = 0.00198 \end{aligned}\]Therefore, we have:
\[\begin{aligned} P(R_T|G_T) &= \frac{0.00197_{TTT} + 0.1584_{TFT}}{0.00198_{TTT}+0.288_{TFF}+0.1584_{TFT} + 0.0_{TFF}} \approx 35.77\% \end{aligned}\]