Permutation:
The permutation indicates how many different ordered arrangements can be made from a set of \(n\) items, calculated by:
\[\begin{equation} P(n) = n! \end{equation}\]Combination:
The combination indicates how many ways to select \(k\) items from a set of \(n\) items (\(k < n\)) without order arrangement, calculated by:
\[\begin{equation} \begin{aligned} \begin{pmatrix}n\\ k\end{pmatrix} = C(n,\ k) = \frac{n!}{k!(n-k)!} \end{aligned} \end{equation}\]For any positive \(n\) and \(k\) with \(k \leq n\), we also have:
\[\begin{aligned} \begin{pmatrix}n\\ k\end{pmatrix} = \begin{pmatrix}n\\ n - k\end{pmatrix} \end{aligned}\]and
\[\begin{aligned} k\begin{pmatrix}n\\ k\end{pmatrix} = n\begin{pmatrix}n-1\\ k-1\end{pmatrix} \end{aligned}\]\(k\)-permutations of \(n\):
The \(k\)-permutation of \(n\) indicates many ways to select \(k\) items from a set of \(n\) items (\(k < n\)) with order arrangement, calculated by:
\[\begin{equation} \begin{aligned} P(n,\ k) = \frac{n!}{(n-k)!} \end{aligned} \end{equation}\]The binomial theorem:
\[\begin{equation} (x + y)^n = \sum_{k=0}^n \begin{pmatrix}n\\ k\end{pmatrix}x^ky^{n-k} \end{equation}\]De Morgan’s Law:
\[\begin{equation} \begin{aligned} (A\cup B)^c =A^c \cap B^c \\ \\ (A\cap B)^c =A^c \cup B^c \end{aligned} \end{equation}\]General form:
Given a set of events \(A_1, \ A_2, \cdots, \ A_n\), we have:
\[\begin{aligned} \left(\bigcup_{i=1}^n A_i\right)^c = \bigcap_{i=1}^n A_i \end{aligned}\] \[\begin{aligned} \left(\bigcap_{i=1}^n A_i\right)^c = \bigcup_{i=1}^n A_i \end{aligned}\]Naive definition of probability:
\[P_\text{naive}(A) = \frac{|A|}{|S|} = \frac{\text{number of outcomes favorable to }A}{\text{total number of outcomes in }S}\]General definition of probability:
A probability space consists of a sample space \(S\) and a probability function \(P\) which takes an event. \(A \subseteq S\) (\(A\) is the subset of \(S\)) as input and returns \(P(A)\), a real number between \(0\) and \(1\), as output. The function \(P\) must satisfy the following axioms:
If \(A_1, \ A_2, \cdots\) are disjoint events (mutually exclusive: \(A_i \cap A_j = \emptyset\) for \(i \neq j\)), then
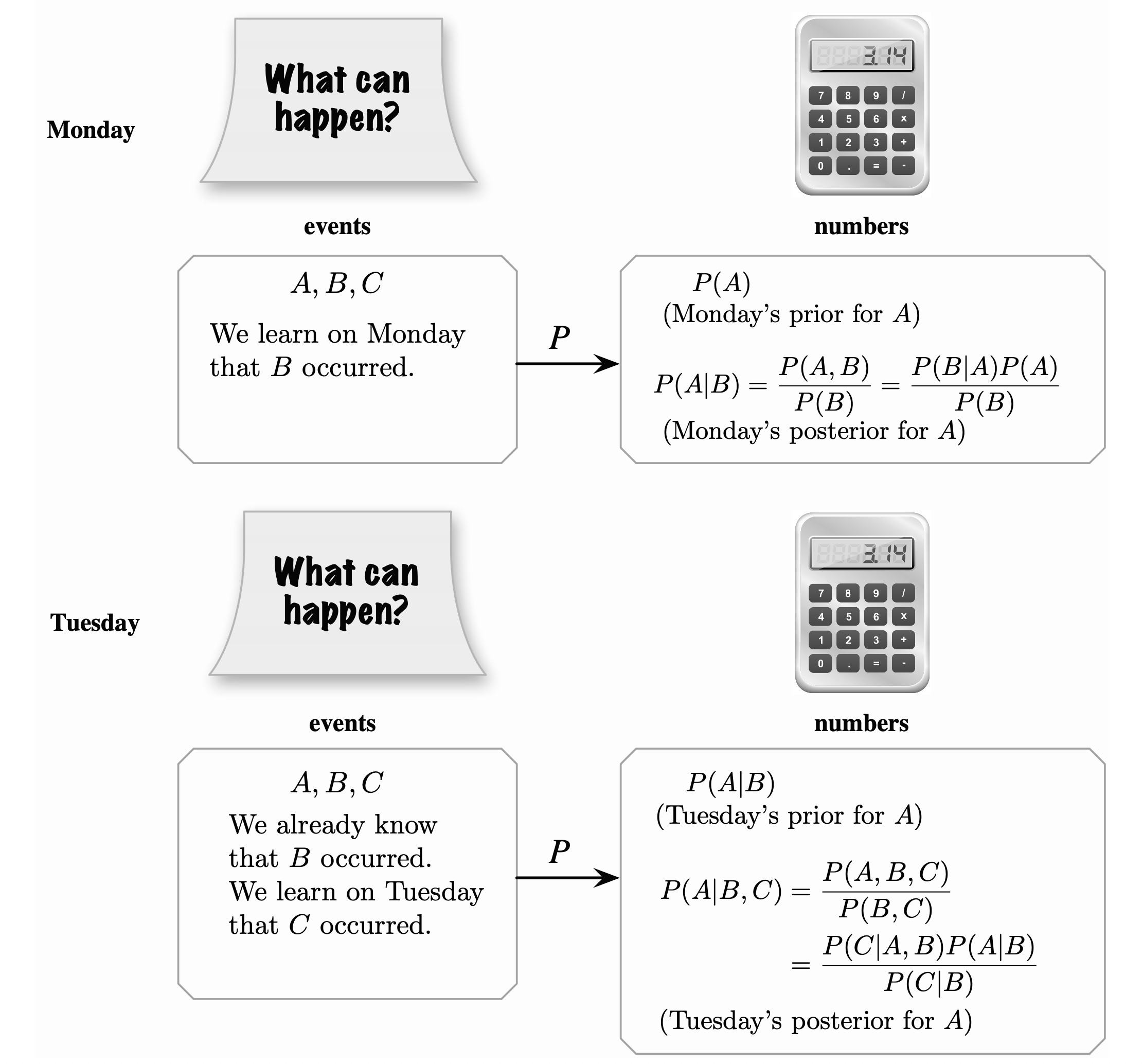
\[P\left(\bigcup_{j=1}^\infty A_j\right) = \sum_{j=1}^\infty P(A_j)\]With two events A and B, the probability of \(A\) given that the event \(B\) already happened is the “conditional probability of A given B” \(P(A\mid B)\), calculated by:
\[\begin{equation} P(A\mid B) = \frac{P(A\cap B)}{P(B)} \end{equation}\]Example:
Multiplication rule: The joint probability of having both \(A\) and \(B\) occur is:
\[\begin{equation} P(A\cap B) = P(A, \ B) = P(A\mid B)\cdot P(B) \end{equation}\]Additional rule: The probability that two events \(A\) or \(B\) occur is:
\[\begin{equation} P(A\cup B) = P(A) + P(B) - P(A \cap B) \end{equation}\]Special cases:
The cases with 3 events \(A\), \(B\), and \(C\):
\[\begin{aligned} P(A,B,C) &= P(A)\cdot P(B \mid A) \cdot P(C\mid A, B) \\ P(A \cup B \cup B) &= P(A) + P(B) + P(C) \\ & \quad - P(A \cap B) - P(A \cap C) - P(B \cap C) \\ & \quad + P(A \cap B \cap C) \end{aligned}\]\(A\) and \(B\) are two independent events if:
\[P(A \cap B) = P(A) \cdot P(B)\]If \(P(A) >0\) and \(P(B)> 0\), then:
\[P(A\mid B) = P(A)\] \[P(B\mid A) = P(B)\]If \(A\) and \(B\) are independent, then \(A\) and \(B^c\) are independent, \(A^c\) and \(B\) are independent, and \(A^c\) and \(B^c\) are independent.
Assume that \(A\), \(B\), and \(C\) are three events. We say that events A and B are independent given event C if:
\[\begin{equation} P(A, B \mid C) = P(A \mid C) \cdot P(B \mid C) \end{equation}\]“Independence” ≠ “Conditional independence”
“Event A and B are independent” does not mean that “A and B are independence given event C”

Events A and B can be dependent and yet they are independent given an event C

With Bayes’s Theorem, \(P(A \mid B)\) can be calculated by:
\[\begin{equation} P(A\mid B) = \frac{P(B|A)\cdot P(A)}{P(B)} \end{equation}\]Odd form:
\[\frac{P(A \mid B)}{P(A^c \mid B)} = \frac{P(B \mid A)}{P(B \mid A^c)} \cdot \frac{P(A)}{P(A^c)}\]where \(A^c\) is the event that \(A\) does not hold
With 3 events \(A, \ B, \ C\), we have:
\[\begin{aligned} P(A \mid B, C) &= \frac{P(B \mid A, C) \cdot P(A \mid C)}{P(B \mid C)} \\&= \frac{P(A,B,C)}{P(B \mid C)} = \frac{P(B, C\mid A) \cdot P(A)}{P(B, C)} \end{aligned}\]Understand better Bayes’s theorem:
In September, the probability of a rainy day is \(0.6\). The probability there is a cloudy day is \(0.3\). The probability that there are clouds on a rainy day is \(0.4\). Therefore, the probability that there is a rainy day when the sky cloud is:
\[P(rain \mid cloud) = \frac{P(rain) \cdot P(cloud \mid rain)}{P(cloud)} = \frac{0.6 \times 0.4}{0.3} = 0.8\]A particular test when someone has been using cannabis is \(90\%\) sensitive, leading to the true positive rate being \(0.9\), the test is also \(80\%\) specific, meaning the true negative rate is \(0.8\). Therefore, the test correctly identifies \(80\%\) of non-user as non-user. Assuming for a group of people, there are \(5\%\) that use cannabis, which is \(0.5\) prevalence. The possibility that random people test correctly as a cannabis user is:
\[P(User \mid Positive) = \frac{P(Positive\mid User)\cdot P(User)}{P(Positive)} = \frac{0.9 \times 0.05}{0.08} = 0.19\]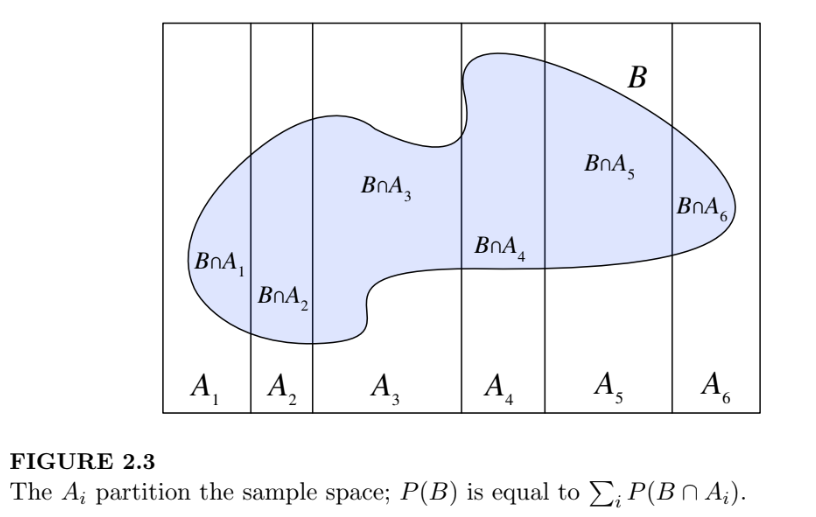
Given an event space:
\[\Omega = B_1 \cup B_2 \cup B_3 \cup \cdots \cup B_m\]with an arbitrary event \(B \in \Omega\), we have the Law of Total Probability:
\[\begin{equation} \begin{aligned} P(B) &= \sum_{i=1}^mP(B\cap A_i) \\ &= \sum_{i=1}^mP(B\mid A_i) \cdot P(A_i) \end{aligned} \end{equation}\]Simpson’s Paradox

With \(A\) = {complication rates of senior doctors}
\[\begin{aligned} P(A) &= P(A \mid easy) \cdot P(easy) + P(A \mid hard) \cdot P(hard) \\ &= 0.052 \times \frac{213}{315} + 0.127 \times \frac{102}{315} = 0.076 \end{aligned}\]With \(B\) = {complication rates of junior doctors}
\[\begin{aligned} P(B) &= P(B \mid easy) \cdot P(easy) + P(B \mid hard) \cdot P(hard) \\ &= 0.067 \times \frac{3169}{3375} + 0.155 \times \frac{206}{3375} = 0.072 \end{aligned}\]Thus, we observe that the reason for Simpson’s paradox is:
In the standard case with two events \(A\), \(B\), with the Law of Total Probability, \(P(B)\) can be calculated by:
\[\begin{equation} P(B) = P(B \mid A) \cdot P(A) + P(B|A^c) \cdot P(A^c) \end{equation}\]With Bayes’s Theorem:
\[P(A \mid B) = \frac{0.05 \times 0.5}{0.52} \approx 0.048 = 4.8\%\]Bayesian inference is a method of statistical inference in which Bayes’s Theorem is used to update the probability of a hypothesis as more data become available:
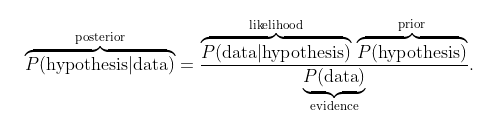
Or:
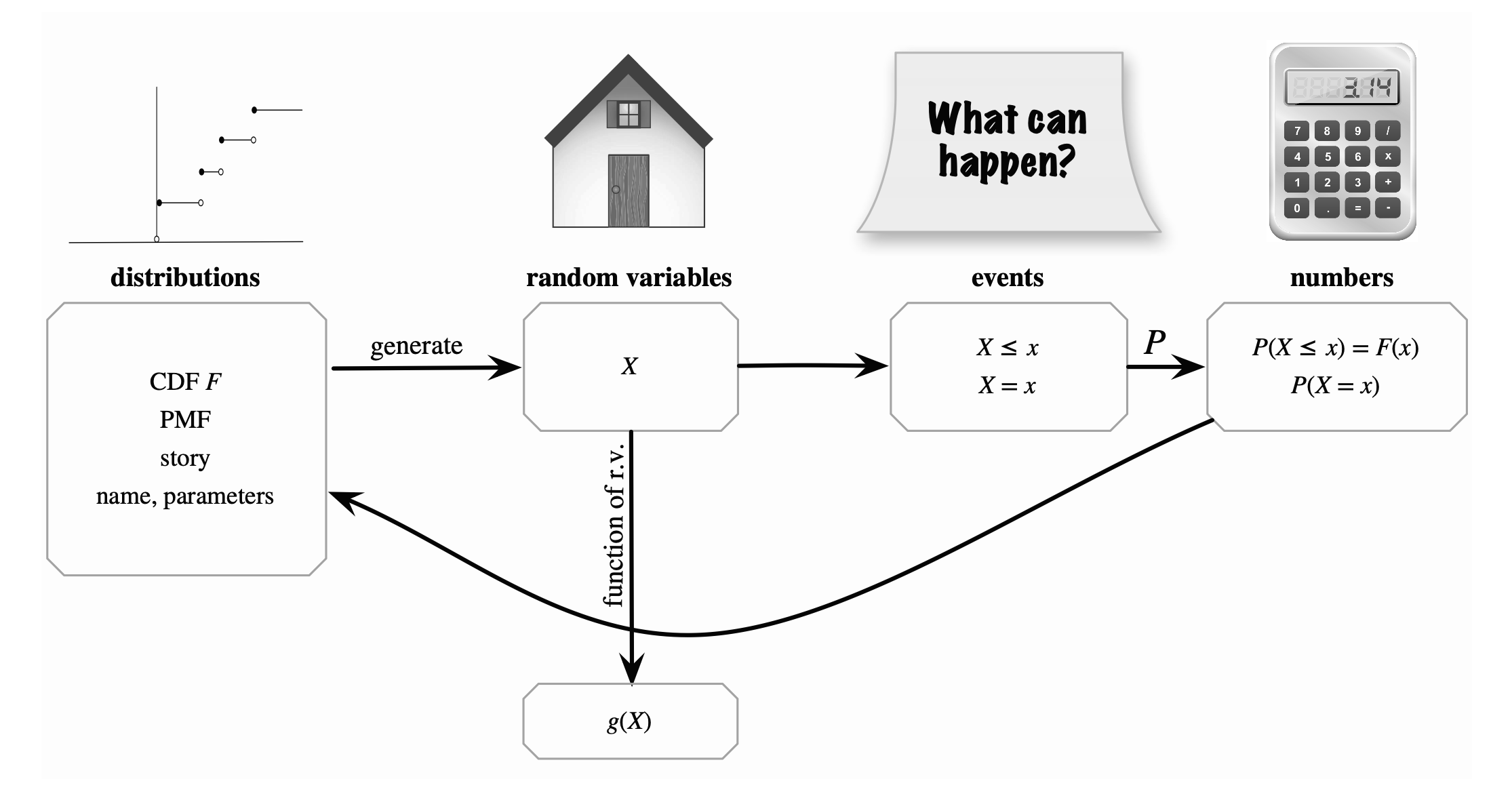
\[Posterior = Likelihood × Prior ÷ Evidence\]Given an experiment with sample space \(\Omega\), a random variable(s) (r.v.) is a measurable function \(X:S → E\) from a set of possible outcomes \(S \in \Omega\) to the real number \(E \in \mathbb{R}\)
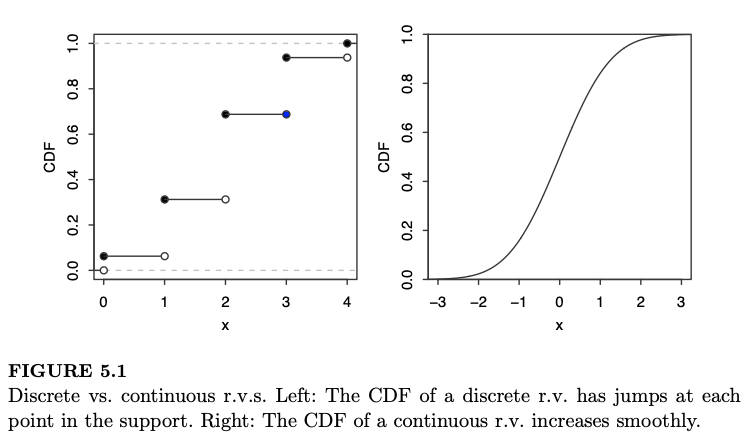
For a discrete random variable \(X\), the probability mass function (p.m.f.) of \(X\) is the function \(p(a)\) gives the probability that a \(X\) takes on the value \(a\):
\[\begin{equation} p(a) = P(X = a) \end{equation}\]The cumulative distribution function (c.d.f.) of a random variables \(X\) (or more simply, the distribution function of \(X\)) is the function \(F_X(a)\) given by:
\[\begin{equation} F_X(a) = P(X \le a)= \underset{X \le a}{\sum}\ p(X) \qquad \qquad -\infty < x < \infty \end{equation}\]Example 1: Suppose that we have an experiment of tossing the coin 3 times. Then we have
\(\Omega = \{HHH, \ HHT, \ HTH, \ HTT, \ THH, \ THT,\ TTH, \ TTT \}\).
If we let \(X\) denote the number of heads that appear, then \(X\) is a discrete random variable that takes one of the values \(E =\{0,..,3\}\).
Example 2: The p.m.f. of a random variable \(X\) is given by \(p(i) = c \frac{\lambda^i}{i!}, \ i = 0, 1, 2,\cdots,\) where \(\lambda\) is some positive value. Find (a) \(P(X=0)\) and \(F(3)\):
Since \(\sum_{i=0}^\infty p(i) = 1\), we have:
\[c\sum_{i=0}^\infty\frac{\lambda^i}{i!} = 1\]however, because \(e^x = \sum_{i=0}^\infty\frac{\lambda^i}{i!}\), then we have:
\[ce^\lambda = 1 \quad \Rightarrow \quad c = e^{-\lambda}\]Hence: \(P(X = 0) = e^{-\lambda}\frac{\lambda^0}{0!} = e^{-\lambda}\)
\[\begin{aligned} F(3) &= \sum_{X \leq 3}P(X) = P(0) + P(1) + P(2) + P(3)\\ &= e^{-\lambda} + \lambda e^{-\lambda} + \frac{\lambda^2 e^{-\lambda}}{2} + \frac{\lambda^3 e^{-\lambda}}{6} \\ &= \frac{\lambda^3 + 3 \lambda^2 + 6 \lambda + 6}{6}e^{-\lambda} \end{aligned}\]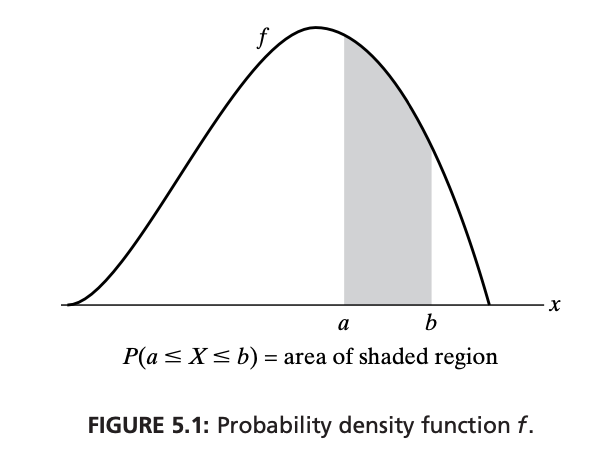
For a continuous r.v. \(X\) with c.d.f. \(F\), the probability density function (p.d.f.) \(f(x)\) of \(X\) is the derivative of \(F\), given by \(f(x) = F’(x)\). Thus, the p.d.f. \(f(x)\) can be defined for all real \(x \in (- \infty, \ \infty)\), having the property that, for any set \(B\) of real numbers:
\[\begin{equation} P(X \in B) = \int_B f(x)\ dx \end{equation}\]Special cases:
\[\begin{aligned} &P\left(X = a\right) = \int_{a}^{a} f(x) \ dx = 0 \\ &P\left(a \le X \le b\right) = \int_{a}^{b} f(x) \ dx \end{aligned}\]p.d.f. to c.d.f.: The c.d.f. \(F(a)\) of continuous r.v. \(X\) given the p.d.f. \(f(x)\) is calculated by:
\[\begin{equation} F(a) = P(X \le a) = \int_{-\infty}^a f(x)\ dx \end{equation}\]Examples:
Example 1: The amount of time in hours that a computer functions before breaking down is a continuous random variable \(X\) with the probability density function given by:
\[\begin{aligned} f(x) = \begin{cases} C(4x - 2 x^2) & 0 < x < 2 \\ 0 &\text{otherwise} \end{cases} \end{aligned}\]What is the value of \(C\) and calculate \(P(X > 1)\)?
Solution:
Since \(f(x)\) is a p.d.f., we must have:
\[\begin{aligned} \int_{-\infty}^{\infty} f(x) \ dx &= 1 \\ \Leftrightarrow \ C\int_{-0}^{2} (4x - 2x^2) \ dx &= 1 \\ \Leftrightarrow \ C\left[2x^2 - \frac{2x^3}{3}\right]\Bigg|_{x=0}^{x=2} &= 1 \\ \Rightarrow \ C &= \frac{3}{8} \end{aligned}\]Integrate the p.d.f. from \(1\) to \(+ \infty\), and we have:
\[\begin{aligned} P(X > 1) = \int_1^\infty f(x) \ dx = \frac{3}{8} \int_1^2(4x-2x^2) \ dx = \frac{1}{2} \end{aligned}\]Example 2: A continuous random variable \(X\) follows the Logistic distribution with the following c.d.f.:
\[\begin{aligned} F(X) = \frac{e^x}{1 + e^x}, \qquad x \in \mathbb{R} \end{aligned}\]Find the p.d.f. \(f(x)\) and \(P(-2 < X < 2)\):
Solution:
To obtain the p.d.f., we differentiate the c.d.f., which gives:
\[\begin{aligned} f(x) = F(X)' = \frac{d}{dx} \left(\frac{e^x}{1 + e^x}\right) = \frac{e^x}{(1 + e^x)^2} \end{aligned}\]Integrate the p.d.f. from \(-2\) to \(2\), and we have:
\[\begin{aligned} P(-2 < X < 2) = \int_{-2}^2\frac{e^x}{(1+e^x)^2} \ dx = F(2) - F(-2) \approx 0.76 \end{aligned}\]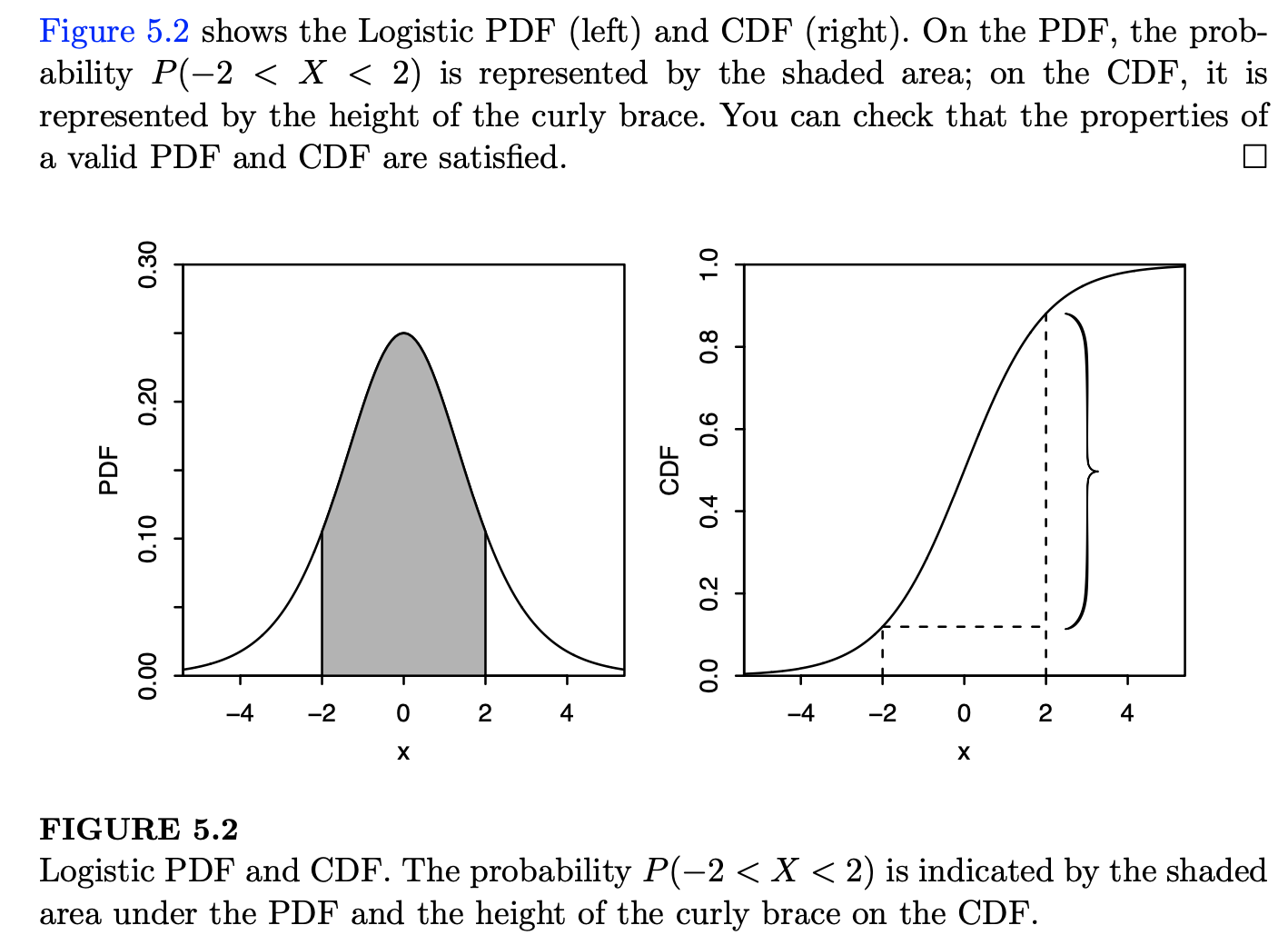
Therefore, two random variables \(X\) and \(Y\) are independent for all \(x, y \in \mathbb{R}\) if:
\[\begin{equation} F_{X, Y}(x, y) = F_X(x)\cdot F_Y(y) \qquad \text{for all} \ x, y \end{equation}\]Equivalently, in the discrete case, given the p.m.f. \(P(X=x)\) and \(P(Y = y)\) and the joint probability mass function \(P(X = x, Y = y)\) exist:
\[P(X = x, Y = y) = P(X=x)\cdot P(Y=y)\]Or equivalently, in the continuous case, given the p.d.f. \(f_X(x)\) and \(f_Y(y)\) and the joint probability density functyion \(f_{X,Y}(x,y)\) exist:
\[f_{X, Y}(x, y) = f_X(x)\cdot f_Y(y)\]Two random variables \(X\) and \(Y\) are conditionally independent given a random variable \(Z\) for all \(x, y \in \mathbb{R}\) and all \(z\) in the support of \(Z\) if:
\[\begin{equation} F_{X, Y \mid Z=z}(x, y) = F_{X \mid Z = z}(x) \cdot F_{Y\mid Z = z}(y) \qquad \text{for all } \ x, y, z \end{equation}\]Equivalently, in the discrete case, for any \(x, y \in \mathbb{R}\) and \(z \in \mathbb{R}\) with the p.m.f. \(P(Z=z) > 0\):
\[P(X = x, Y = y | Z = z) = P(X=x | Z=z)\cdot P(Y=y|Z=z)\]Or equivalently, in the continuous case, for all \(x, y \in \mathbb{R}\) and \(z \in \mathbb{R}\) with the p.d.f. \(f_Z(z) >0\):
\[f_{X, Y \mid Z}(x, y|z) = f_{X\mid Z}(x|z)\cdot f_{Y\mid Z}(y|z)\]Denote \(X\) and \(Y\) are, respectively, the time past 12:00 that the man and the women arrive. Thus, \(X\) and \(Y\) are two independent random variables, each of which is uniformly distributed over \((0, \ 60)\). We have the desired probability. \(P(X + 10 < Y) + P(Y + 10 < X) = 2P(X + 1 < Y)\) (by symmetry), calculated as follows:
\[\begin{aligned} 2P(X + 10 < Y) &= \underset{x + 10 < y}{\int\int}f(x,y)dx \ dy\\ &= 2\underset{x + 10 < y}{\int\int}f_X(x)f_Y(y)dx \ dy\\ &= 2\int_10^60\int_0^{y-10}\left(\frac{1}{60}\right)^2 dx \ dy \\ &= \frac{2}{360}\int_10^60(y-10)dy\\ &= \frac{25}{36} \end{aligned}\]More generally, given the weight \(p_1, \ p_2, \cdots, p_n\) that add up to 1, the weighted mean (or mean as weighted sum) of \(x_1, \ x_2, \cdots, x_n\) is:
\[\begin{equation} \text{weighted-mean}(x) = \sum_{j=1}^np_j\cdot x_j \end{equation}\]The median is the value that separates the first half and the second half of a sorted data sample, a population, or probabilistic distribution. It also may be considered “the middle” value. Given a list of sorted numbers \(x_1, \ x_2, \cdots, x_n\), there are two ways to find the median:
If \(n\) odd:
\[\text{median}(x) = x_{(n+1)/2}\]If \(n\) even:
\[\text{median}(x) = \frac{x_{(n/2)}+x_{(n+1)/2}}{2}\]
The expectation (or expected value) indicates the center value of the distribution of a random variable.
Discrete random variable:
Given \(X\) is a discrete random variable having a p.m.f. \(p(x)\), then the expectation of \(X\), denoted as \(E[X]\) (or \(\mu\)), is defined by:
\[\begin{equation} \mu = E[X] = \sum_{x:p(x)>0}x\cdot p(x) \end{equation}\]Or it can also be written, if distinct possible values of \(X\) are \(x_1, \ x_2, \cdots, x_n\), by:
\[E(X) = \sum_{j = 1}^nx_j\cdot P(X=x_j)\]If two random variables \(X\) and \(Y\) share the same distribution, then:
\[E[X] = E[Y]\]For any random variables \(X, \ Y\) , and any constant \(c\), we have:
\[\begin{aligned} E[X + Y] &= E[X] + E[Y] \\ E[cX] &= c \cdot E[X] \end{aligned}\]Example: A school class of 120 students is driven in 3 buses to a symphonic performance. There are 36 students on one of the buses, 40 on another, and 44 on the third bus. When the buses arrive, one of the 120 is randomly chosen. Let \(X\) denote the number of students on the bus that are randomly chosen. Find the expectation of \(X\).
Thus, we have:
\[E[X] = 36\times\frac{3}{10} + 40\times\frac{1}{3} + 44\times\frac{11}{30} = \frac{1208}{30} = 40.2667\]If \(X\) is a discrete random variable that takes on one of the values \(x_i, \ i \geq 1\), with respective probabilities \(p(x_i)\), then, for any real-valued function \(g\) from \(\mathbb{R}\) to \(\mathbb{R}\):
\[\begin{equation} E[g(X)] = \sum_i g(x_i)P(X = x_i) = \sum_i g(x_i)p(x_i) \end{equation}\]We have:
\[\begin{aligned} E[X^2 + 3] &= [(-1)^2 + 3] \times 0.2 + (0^2 + 3) \times 0.5 + (1^2 + 3) \times 0.3 \\ &= 4 \times (0.2 + 0.3) + 3 \times 0.5 = 3.5 \end{aligned}\]Continuous Random Variable:
Given \(X\) is a continuous random variable having the p.d.f. \(f(x)\), then, the expected value of \(X\) is:
\[\begin{equation} \mu = E[X] = \int_{-\infty}^{+\infty}xf(x) \ dx \end{equation}\]which is the balancing point of the p.d.f..
LOTUS for continuous r.v.:
If \(X\) is a continuous random variable and \(g\) is a function from \(\mathbb{R}\) to \(\mathbb{R}\), then:
\[\begin{equation} E[g(X)] = \int_{-\infty}^{+\infty}g(x)f(x) \ dx \end{equation}\]Given the expectation value \(\mu = E[X]\) of a random variable \(X\), the variance is calculated by:
\[\begin{equation} \begin{aligned} \text{Var}(X) &= E[(X - \mu)^2]\\ &= E[X^2] - E[X]^2 \end{aligned} \end{equation}\]A useful identity is that for any constant \(a\) and \(b\):
\[\text{Var}(aX + b) = a^2\text{Var}(X)\]Also, variance is not linear, which means:
\[\text{Var}(X + Y) \neq \text{Var}(X) + \text{Var}(Y)\]The square root of the \(\text{Var}(X)\) is called the standard deviation, denoted as \(\text{SD}(X)\) or \(\sigma\), of \(X\):
\[\sigma = \text{SD}(X) = \sqrt{\text{Var}(X)} = \sqrt{E[(X - \mu)^2]}\]Discrete random variable:
Based on formula \((21)\) of the expected value \(\mu\) of a discrete random variable \(X\), the variance is calculated by:
\[\begin{equation} \sigma^2 = \text{Var}(X) = \sum_{i=1}^np(x_i)\cdot(x_i - \mu)^2 \end{equation}\]Continuous random variable:
Based on formula \((23)\), with the expected value \(\mu\) of a continuous random variable \(X\), we have:
\[\begin{equation} \sigma^2 = \text{Var}(X) = \int_{i=1}^n(x_i - \mu)^2f(x) \ dx \end{equation}\]Example: Find \(\mu\) and \(\sigma^2\) of a random variable \(X\), given the p.d.f.:
\[\begin{aligned} f(x) = \begin{cases} 2x \quad &\text{if} \quad 0 \leq x \leq 1\\ 0 &\text{otherwise} \end{cases} \end{aligned}\]We have:
Expectation:
\[\begin{aligned} \mu = E[X]= \int_0^1xf(x) \ dx = \int_0^1 2x^2 \ dx = \frac{2}{3} \end{aligned}\]Variance:
\[\begin{aligned} E[X^2] &= \int_0^1x^2f(x) \ dx = \int_0^1 2x^3 \ dx = \frac{1}{2}\\ \\ \sigma^2 &= \text{Var}(X) = \frac{1}{2} - \left(\frac{2}{3}\right)^2 = \frac{1}{18} \end{aligned}\]A probability distribution is a statistical model that describes all the probabilities of all possible events that a random variable can take within range. Some distributions are so ubiquitous in probability and statistics that they have their own name.
A random variable \(X\) that is said to have the distribution \(A\) with parameter \(p\) is usually denoted as
\[X \sim A(p)\]which the symbol \(\sim\) is read as “is distributed as”
Let \(C\) be a finite, nonempty set of numbers, all values in \(C\) are equally likely. Choose one of these numbers uniformly at random. The random variable of getting a number \(X\) follows the Discrete Uniform distribution with parameter \(C\), denoted by \(X \sim \text{DUnif}(C)\). The p.m.f. of the distribution is:
\[\begin{equation} P(X=x) = \frac{1}{|C|} \end{equation}\]Bernoulli distribution:
A discrete random variable \(X\) is said to have the Bernoulli distribution with parameter \(p\) if \(X\) has only two outcomes \(X = 0\) and \(X = 1\), following the probability mass function of X given by:
\[\begin{equation} \begin{cases} p(1) = P(X=1) = p \\ p(0) = P(X=0) = 1 - p \end{cases} \end{equation}\]where \(0 \leq p \leq 1\) is the probability that the trial success. Therefore, \(X \sim \text{Bern}(p)\)
Binomial distribution:
Suppose that there are \(n\) independent Bernoulli trials performed with the same success probability \(p\). If discrete random variable \(X\) represents the number of successes that occur in the \(n\) trials, then \(X\) follows the Binomial distribution with parameters \(n\) and \(p\), denoted by \(X \sim \text{Bin}(n, \ p)\), where \(n\) is a positive number with \(0 \leq p \leq 1\). Then, the p.m.f. of \(X\) is:
\[\begin{equation} p(i) = \begin{pmatrix}n\\ i\end{pmatrix}p^i(1-p)^{n-i} \qquad \text{where } i = 0, 1,\cdots,n \end{equation}\]By the binomial theorem, all the probabilities sum to \(1\); that is:
\[\begin{aligned} \sum_{i=0}^\infty p(i) = \sum_{i=0}^n\begin{pmatrix}n\\ i\end{pmatrix}p^i(1-p)^{n-i} = [p + (1 - p)]^n = 1 \end{aligned}\]If \(X\) is the number of defective screws in a package, then \(X \sim \text{Bin}(10, \ 0.02)\). Hence, the probability that a package will have to be replaced is:
\[1 -p(0) - p_1) = 1 - \begin{pmatrix}10\\ 0\end{pmatrix}(0.02)^0 (0.98)^10 - \begin{pmatrix}10\\ 1\end{pmatrix}(0.02)^1 (0.98)^9 \approx 0.016\]Expectation and variance:
If \(X \sim \text{Bin}(n, \ p)\), then:
\[\begin{aligned} E[X] &= np\\ \text{Var}(x) &= np(1-p) \end{aligned}\]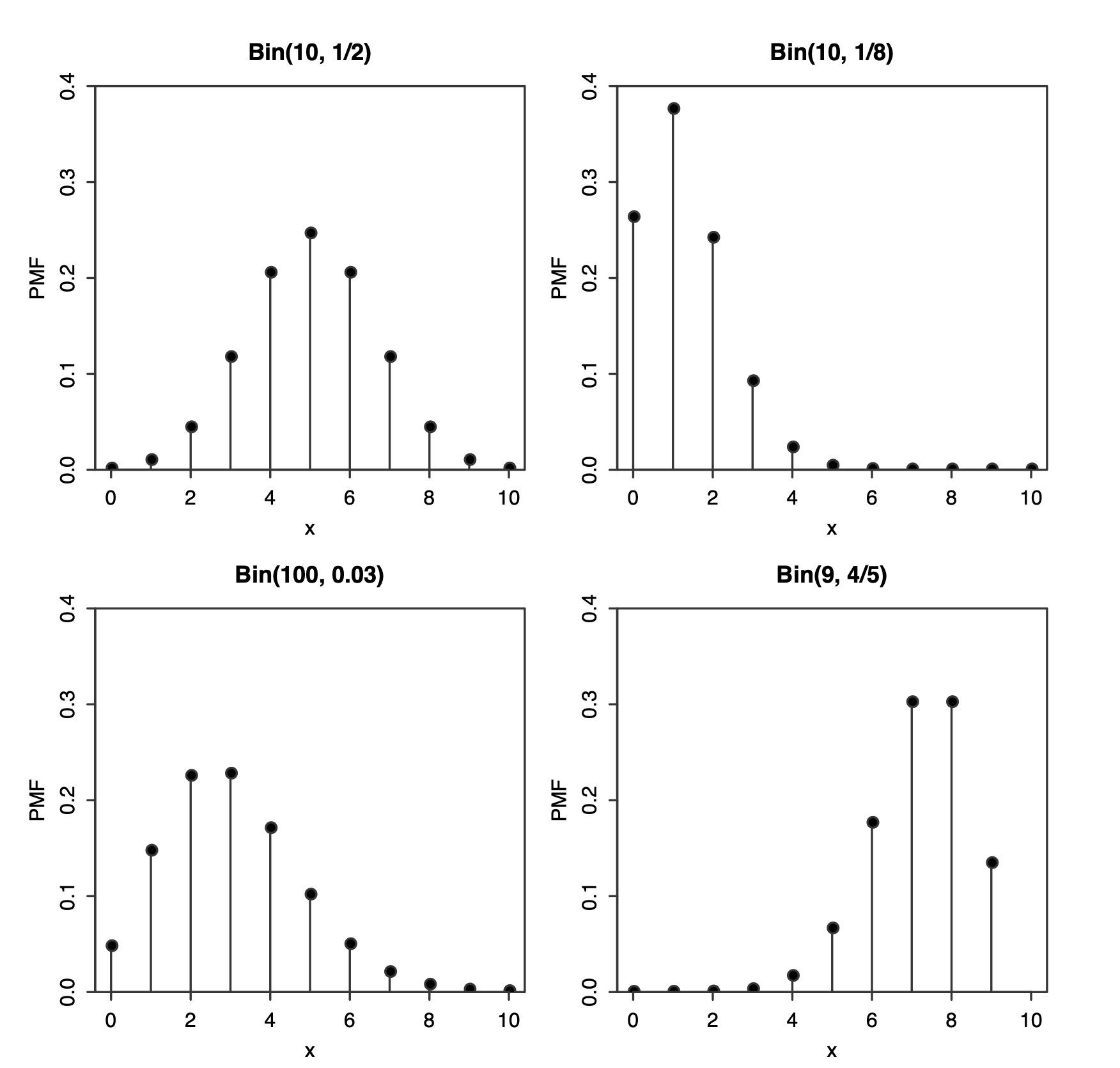
Categorical distribution:
Categorical distribution is the generalization of Bernoulli distribution. Thus, sometimes it can be referred as a generalized Bernoulli distribution or multinoulli distribution.
Given \(X\) is a discrete random variable that follows the Categorical distribution, \(X\) then takes on one of \(X\sim \text{Cat}_k(k,\ \boldsymbol{p})\) possible categories, with the probability of each category separately specified. Therefore: \(X\sim \text{Cat}_k(k,\ \boldsymbol{p})\) where \(\boldsymbol{p} = [p_1,\cdots, \ p_k]\).
The probability mass function of Categorical distribution is:
\[\begin{equation} p(i|\boldsymbol{p}) = \prod_{i=1}^kp_i^{[x = i]} \end{equation}\]where \([x = i]\) is in the Inverson bracket, indicates that:
\[[x=i] = \begin{cases} 1 \quad & \text{if } x=i \\ 0 & \text{otherwise} \end{cases}\]Multinomial distribution:
It is the generalization of Binomial distribution, where multiple independent trials follow the Categorical distribution. Given \(X\) is a discrete random variable that follows the Multipomial distribution consisting of \(n\) Categorical trials that outcome \(k\) results independently, we denote \(X \sim \text{Mult}_k(n, \ \boldsymbol{p})\), with the p.m.f.:
\[\begin{equation} P(X_1=n_1,\ X_2=n_2,\cdots,\ X_k = n_k)= \frac{n!}{n_1!n2!\cdots n_k!}p_1^{n_1}p_2^{n_2}\cdots p_k^{n_k} \end{equation}\]whenever \(\begin{aligned}\sum_{i=1}^kn_i =n\end{aligned}\), with \(n_i\) is the number that result \(i\)-th happened.
Example: Suppose 9 fair dice are rolled. The probability that \(1\) appears three times, \(2\) and \(3\) appear twice each, \(4\) and \(5\) once each, and \(6\) not at all is:
\[\begin{aligned} \frac{9!}{3!2!2!1!1!0!}\left(\frac{1}{6}\right)^3\left(\frac{1}{6}\right)^2\left(\frac{1}{6}\right)^2\left(\frac{1}{6}\right)^1\left(\frac{1}{6}\right)^1\left(\frac{1}{6}\right)^0 = \frac{9!}{3!2!2!}\left(\frac{1}{6}\right)^9 = \frac{1}{419904} \end{aligned}\]Suppose that a sample of size \(n\) is to be chosen randomly without replacement from an urn containing of \(m\) white balls and \(b\) black balls. If we let \(X\) denote the number of white balls selected, then \(X\) is said to have the Hergeometric distribution with parameters \((w, b, n)\), denoted by \(X \sim \text{HGeom}(m,\ b,\ n)\). The p.m.f. of \(X\) is:
\[\begin{equation} P(X = k) = \frac{\begin{pmatrix}m\\k\end{pmatrix}\begin{pmatrix}b\\n-k\end{pmatrix}}{\begin{pmatrix}w+b\\n\end{pmatrix}} \end{equation}\]Example: A purchaser of electrical components buys them in lots of size \(10\). It is his policy to inspect \(3\) components randomly from a lot and to accept the lot only if all \(3\) are non-defective. If \(30\%\) of the lots have \(4\) defective components and \(70\%\) have only 1, what proportion of lots does the purchaser reject?
Let \(A\) denote the event that the purchaser accepts a lot. Now we have:
\[\begin{aligned} P(A) &= P(A|\text{lot have 4 defectives})\frac{3}{10} + P(A|\text{lot have 1 defectives})\frac{7}{10}\\ &= \frac{\begin{pmatrix}4\\0\end{pmatrix}\begin{pmatrix}6\\3\end{pmatrix}}{\begin{pmatrix}10\\3\end{pmatrix}}\frac{3}{10} + \frac{\begin{pmatrix}1\\0\end{pmatrix}\begin{pmatrix}9\\3\end{pmatrix}}{\begin{pmatrix}10\\3\end{pmatrix}}\frac{7}{10} = \frac{54}{100} \end{aligned}\]A discrete random variable has the Poisson distribution with parameter \(\lambda > 0\), denoted by \(X \sim \text{Pois}(\lambda)\), if the p.m.f. of \(X\) is:
\[\begin{equation} p(k) = \frac{e^{-k}\lambda^k}{k!} \end{equation}\]We have the expectation and variance of the Poisson distribution are both equal to \(\lambda\):
\[\begin{aligned} \text{Expectation:} \qquad E[X] &= e^{-\lambda}\sum_{k=0}^\infty k\frac{\lambda^k}{k!} = e^{-\lambda}\sum_{k=1}^\infty k\frac{\lambda^k}{k!}\\ &= \lambda e^{-\lambda}\sum_{k=1}^\infty k\frac{\lambda^{k-1}}{(k-1)!} = \lambda e^{-\lambda}e^\lambda = \lambda \\ \text{Variance:} \qquad E[X^2] &= e^{-\lambda}\sum_{k=0}^\infty k^2\frac{\lambda^k}{k!} = e^{-\lambda}e^\lambda\lambda(1 +\lambda) = \lambda(1 + \lambda)\\ \Rightarrow \quad \text{Var}(x) &= E[X^2] - E[X]^2 = \lambda(1 + \lambda) - \lambda^2 = \lambda \end{aligned}\]Specifically: if \(X \sim \text{Bin}(n, \ p)\) and we let \(n \rightarrow \infty\) and \(p \rightarrow 0\) such that \(\lambda = np\) remains fixed, then the p.m.f. of \(X\) converges to the \(\text{Pois}(\lambda)\) p.m.f.. Therefore:
\[P(X = k) \rightarrow \frac{e^{-\lambda}\lambda^k}{k!}\]Let \(X\) denote the number of errors on this page, we have:
\[\begin{aligned} P(X \geq 1) = 1 - P(X = 0) = 1 - e ^\frac{1}{2}\frac{\frac{1}{2}^0}{0!} \approx 0.393 \end{aligned}\]Therefore, to have a 50-50 chance of having a within-one-day birthday, we have:
\[\begin{aligned} &P(X \geq 1) = 1 - P(X = 0) = 1 - e^{}\approx 0.5 \\ &\Rightarrow e^{-\begin{pmatrix}m \\ 2 \end{pmatrix}\frac{3}{365}} \approx 0.5 \Rightarrow m \approx 14 \end{aligned}\]Similar to the discrete case, a continuous random variable \(X\) follows the continuous Uniform Distribution on the interval \((a, b)\), denoted by \(X \sim \text{Unif}(a,b)\), is a completely random number between \(a\) and \(b\), if its p.d.f. is:
\[\begin{equation} f(x) = \begin{cases} \frac{1}{b-a} \qquad &\text{if } x \in [a,\ b]\\ 0 & \text{otherwise} \end{cases} \end{equation}\]The c.d.f. of the distribution í the accumulated area under the p.d.f., which is
\[F(x) = \begin{cases}0 &\text{if } x \leq a \\ \frac{x-a}{n-a} \qquad &\text{if } x \in [a, \ b] \\ 1 &\text{if } x \geq b \end{cases}\]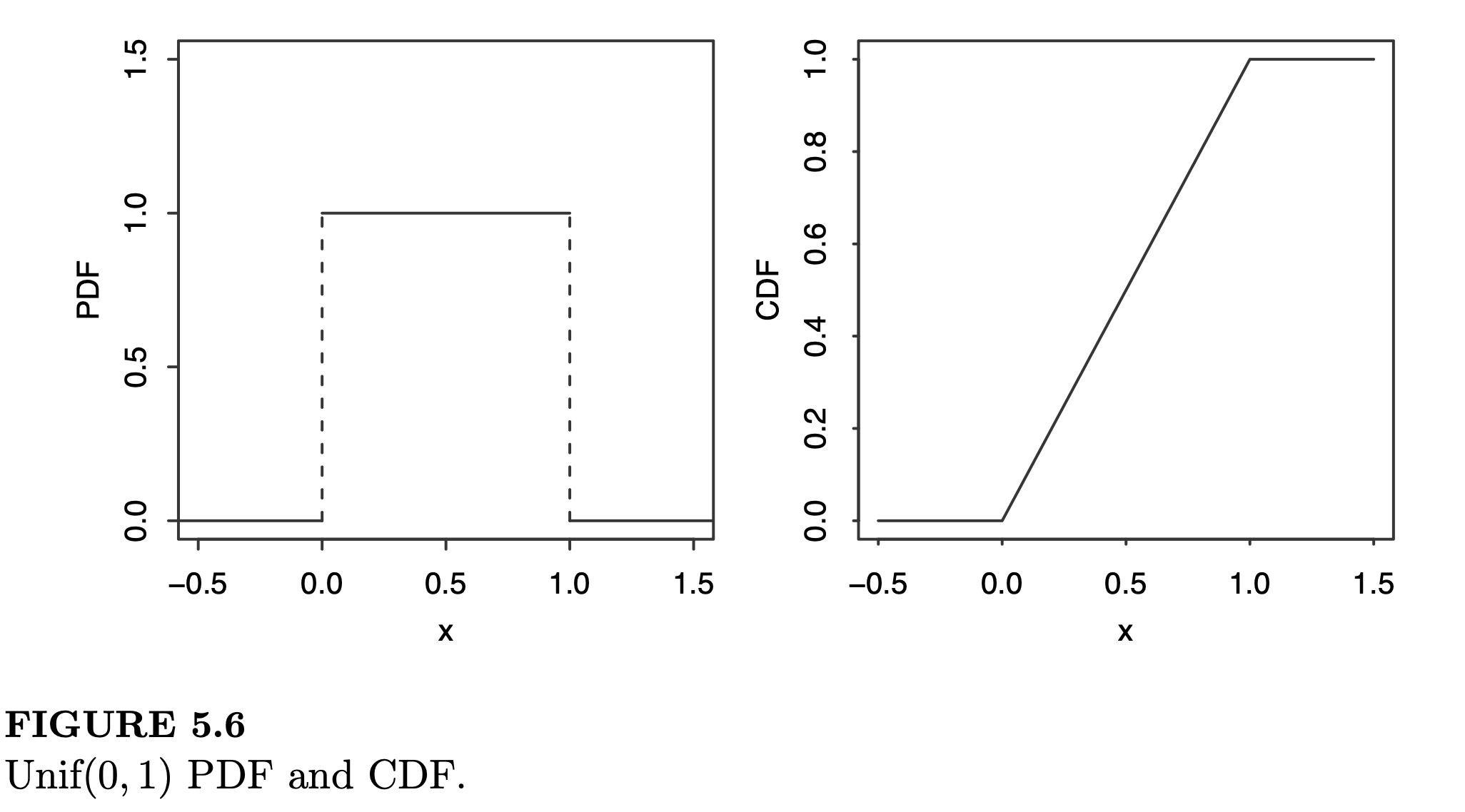
A good example of uniform distribution is an idealized random number generator. However, as every variable has an equal chance of happening, there is an infinity number of points that can exist, even in a small range.
Standard Normal Distribution: A continuous random variable \(Z\) is said to have the standard Normal Distribution \(Z \sim \mathcal{N}(0,1)\) if its p.d.f. is given by:
\[\begin{align} \varphi(z) = \frac{1}{\sqrt{2\pi}}e^{-z^2/2} \end{align}\]The c.d.f. of a Normal Distribution, often denoted as \(\Phi\), is the accumulated area under the p.d.f., calculated by:
\[\begin{equation} \Phi(z) = \int_{-\infty}^z\varphi(t)\ dt = \int_{-\infty}^z\frac{1}{\sqrt{2\pi}}e^{-t^2/2} dt \end{equation}\]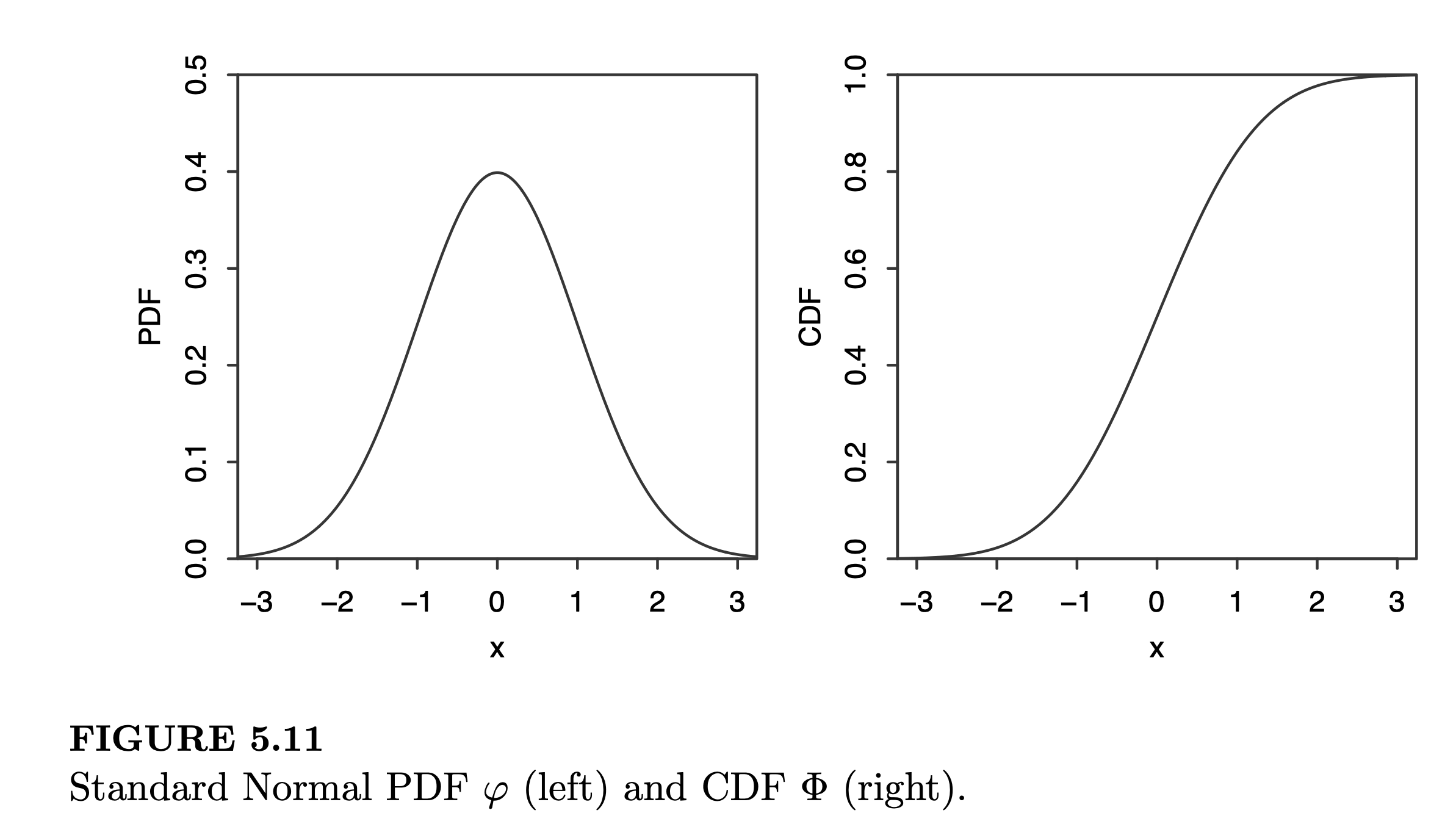
Expectation and Variance:
\[\begin{aligned} E[X] &= \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}ze^{-z^2/2} \ dz \\ & = -\frac{1}{\sqrt{2\pi}}e^{-z^2/2}\big|_{-\infty}^{+\infty}\\ &= 0 \end{aligned}\] \[\begin{aligned} \text{Var}(Z) &= E[Z^2] - E[Z]^2\\ &= \frac{2}{\sqrt{2\pi}}\int_{0}^{+\infty}z^2e^{-z^2/2} \ dx \\ &= \frac{2}{\sqrt{2\pi}}\left(-ze^{-z^2/2}\bigg|_0^\infty + \int_0^\infty e^{-z^2/2} \ dz \right) \\ &= \frac{2}{\sqrt{2\pi}}\left(0 + \frac{\sqrt{2\pi}}{2}\right) = 1 \end{aligned}\]Normal Distribution with variance and expectation: If \(Z \sim \mathcal{N}(0,1)\), a continuous random variable \(X = \mu + \sigma Z\) is said to follow the Normal Distribution with expectation \(\mu\) and variance \(\sigma^2\) , denoted by \(X \sim \mathcal{N}(\mu,\ \sigma^2)\). Thus, its p.d.f. is given by:
\[\begin{equation} f(x) = \varphi \left(\frac{x - \mu}{\sigma}\right)\frac{1}{\sigma}= \frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x - \mu)^2/2\sigma^2} \end{equation}\]
The DeMoivre-Laplace limit theorem: If \(S_N\) denotes the number of successes that occur when \(n\) independent trials perform, each resulting with probability \(p\), then, for any \(a < b\):
\[\begin{aligned} P\left(a \leq \frac{S_n - np}{\sqrt{}np(1-p)}\leq b \right) \rightarrow \Phi(b) - \Phi(a)\\ \end{aligned} \quad \text{as} \quad n \rightarrow \infty\]One example to visualize the theorem is the Galton Board, which can be observed by this GIF:
Because the binomials is a discrete integer-valued random variable, whereas the normal is a continuous random variable, it is best to write \(P(X = i)\) as \(P(i - 1/2 < X < i + 1/2)\) before applying the normal approximation. Doing so gives:
\[\begin{aligned} P(X=20) &= P(19.5 \leq X \leq 20.5)\\ &= P\left(\frac{19.5 - 20}{\sqrt{10}}<\frac{X - 20}{\sqrt{10}}<\frac{20 - 20}{\sqrt{10}}\right)\\ &\approx P\left(-0.16<\frac{X - 20}{\sqrt{10}}<0.16\right)\\ &\approx \Theta(0.16) - \Theta(-0.16) \approx0.1272 \end{aligned}\]On the other hand, the extract result is:
\[\begin{aligned}P(X=20)=\begin{pmatrix}40\\20\end{pmatrix}\left(\frac{1}{2}\right)^{40}\approx 0.1254\end{aligned}\]A continuous random variable X follows the Exponential Distribution \(X \sim \text{Expo}(\lambda)\) with parameter \(\lambda >0\) if its p.d.f. is:
\[\begin{equation} \begin{aligned} f(x) = \lambda e^{-\lambda x} \qquad x > 0 \end{aligned} \end{equation}\]The cossesponding c.d.f. is:
\[F(x)= 1 - e^{-\lambda x} \qquad x > 0\]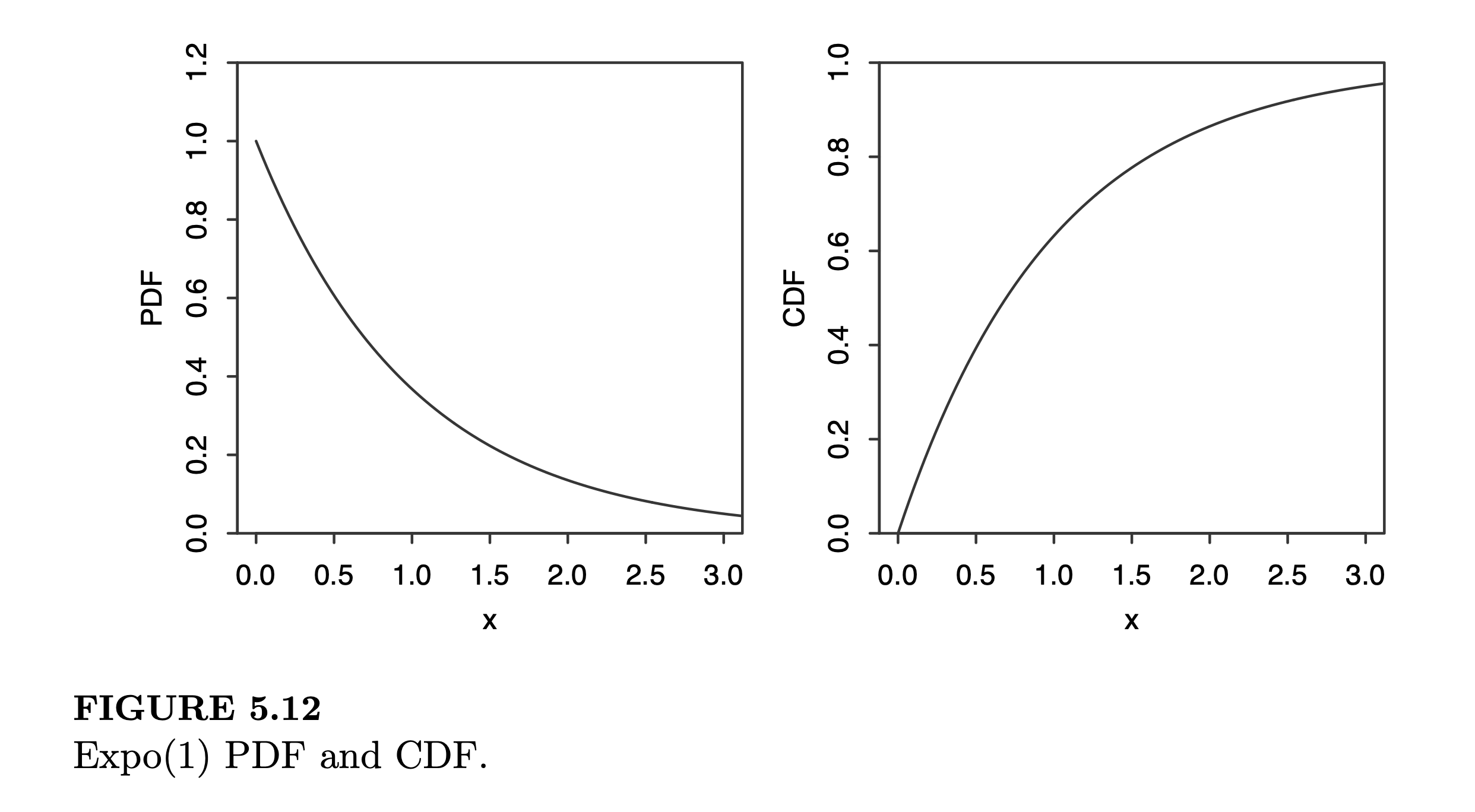
Expectation and variance:
\[\begin{aligned} E[X] = \frac{1}{\lambda};\quad\qquad \text{Var}(X) = \frac{1}{\lambda^2} \end{aligned}\]Example: Suppose that a length of a phone call in minutes is an exponential random variable with \(\lambda = \frac{1}{10}\). If someone arrives immediately ahead of you at a public telephone booth, find the probability that you have to wait: (a) more than 10 minutes; (b) between 10 and 20 minutes:
Let \(X\) denote the length of the call made by the person in the booth, we have:
\[P(X > 10) = 1 - F(10) = e^{-1} \approx 0.368\] \[P(10 < X<20) = F(20) - F(10) = e^{-1} - e^{-2} \approx 0.233\]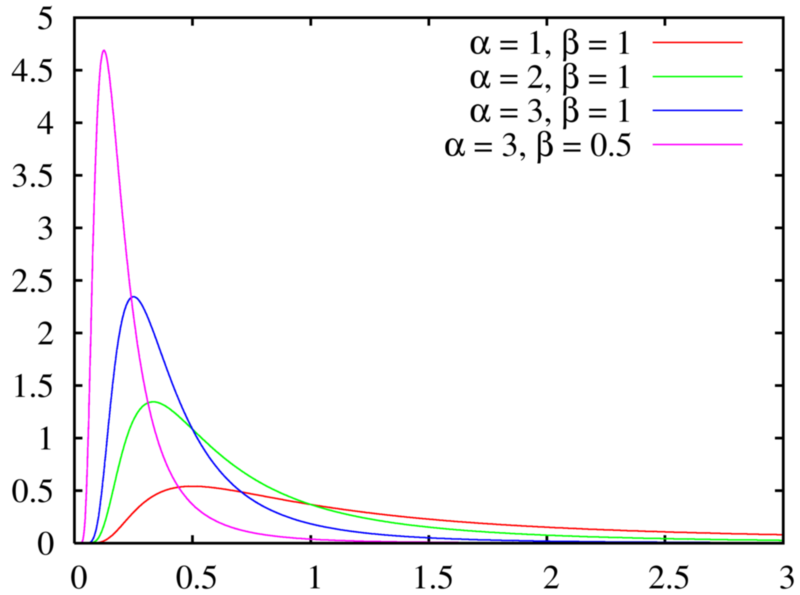
A random variable \(X\) is said to have Gamma distribution with parameter \(\alpha > 0; \ \beta > 0\), denoted as \(X \sim \Gamma(\alpha; \beta)\) if its p.d.f. is given by:
\[\begin{equation} f(x; \alpha, \beta) = \frac{\beta e^{-\beta x}(\beta x)^{\alpha - 1}}{\Gamma(\alpha)} \qquad x > 0 \end{equation}\]where \(\Gamma(\alpha)\), called the gamma function, is calculated by:
For integral values \(\alpha\) (discrete):
\[\Gamma(\alpha) = (\alpha - 1)!\]For real values \(\alpha\) (continuous):
\[\begin{aligned}\Gamma(\alpha) = \int_0^\infty t^{\alpha - 1}e^{-t} \ dt \end{aligned}\]Expectation and variance:
\[\begin{aligned} E[X] = \frac{\alpha}{\beta};\quad\qquad \text{Var}(X) = \frac{\alpha}{\beta^2} \end{aligned}\]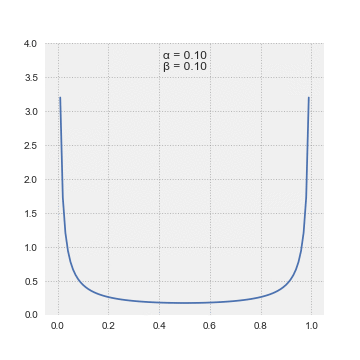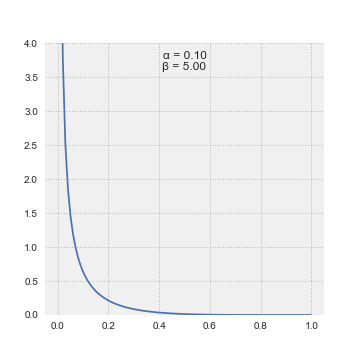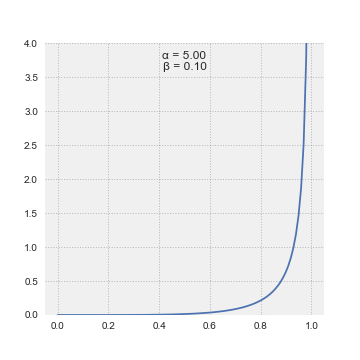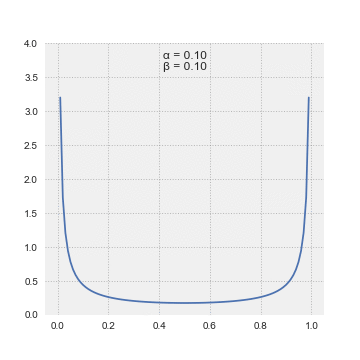
A random variable \(X\) is said to have Beta distribution with parameter \(\alpha > 0; \ \beta > 0\), denoted as \(X \sim \Beta(\alpha; \beta)\) if its p.d.f. is given by:
\[\begin{equation} f(x; \alpha, \beta) =\frac{1}{B(\alpha,\ \beta)}x^{\alpha - 1}(1-x)^{\beta - 1} \qquad 0 \leq x \leq 1 \end{equation}\]where \(\Beta(\alpha, \beta)\), called the beta function, is a normalization constant to ensure that the total probability is \(1\), calculated by:
\[\begin{aligned} B(\alpha, \beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)} = \int_0^1x^{\alpha - 1}(1 - x)^{\beta - 1}\ dx \end{aligned}\]Expectation and variance:
\[\begin{aligned} E[X] = \frac{\alpha}{\alpha + \beta};\quad\qquad \text{Var}(X) = \frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)} \end{aligned}\]